LFM信号的基本参数
一个LFM信号一般包含以下基本参数:脉冲重复周期、脉冲宽度、采样频率、中心频率、信号带宽;仿真回波信号时还需要有以下参数:目标距离、径向速度等;可以计算的参数有:采样周期、回波时延、调频斜率、多普勒频移等。
LFM信号的时间轴仿真
仿真信号时,时间轴的选则非常重要,我习惯将物理时间 t 作为时间轴。
在进行时间轴仿真前需要明确几个参数的具体含义:
脉冲重复周期
Tr:脉冲重复周期指的是从一个信号发射开始到下一个信号发射开始所积累的时间长度,一般为e-4s
脉冲宽度
tau:脉冲宽度指的是在一个脉冲重复周期中有价值的信号时间长度,一般为e-6s
采样频率
fs:采样频率指的是一个采样周期积累的时间的倒数
采样周期
ts: $$ ts=\frac{1}{fs} $$ 采样周期指的是一次采样所积累的时间长度,一般为e-7
发射信号的时间轴仿真

假设有3个 Tr,既 N=3 ,则物理时间轴 t 长度为 N*Tr,因为 t 原点从0开始,所以 t 的范围为 [0, Tr),既 [1, Tr-ts]。间隔为 ts。
t = 0:ts:N * Tr - ts;
为了确保信号只在脉冲宽度范围有效,需要为仿真的完整信号加窗,确保只保留加窗部分的LFM信号。
首先,抽取一个 Tr 的时间长度 t。
t = 0:ts:Tr - ts;
然后,创建一个 t 大小的窗,取名为 rect。
rect = zeros(1, length(t));
之后,将rect窗添加到 t 上。原理是:将 t 时间轴 [0, tau] 部分置为1,其余部分置为0。
for i = 1:length(t)
if t(i) >= 0 && t(i) <= tau
rect(i) = 1;
end
end
最后,使用repmat函数重复rect窗。N 表示 Tr 的个数。
Signal_Radar = repmat(rect, 1, N)
回波信号的时间轴仿真
回波信号指的是雷达发射信号经过目标反弹回来的信号,期间有一个回波时延 t_r ,回波时延的定义如下:
将回波时延加入物理时间轴 t 中,可以用下图表示:
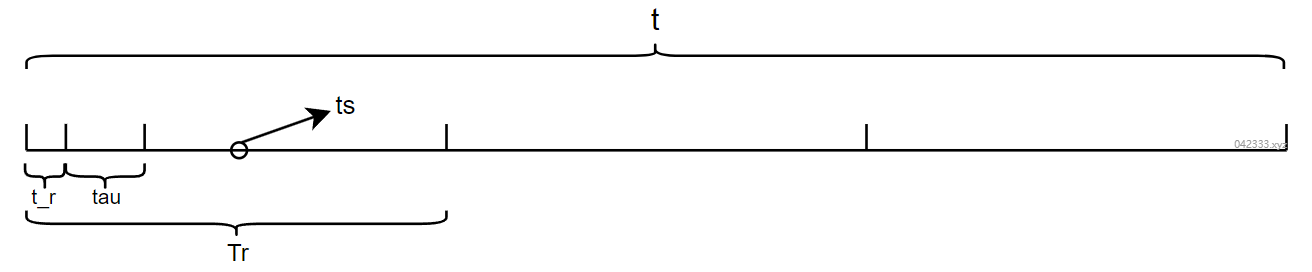
同样的,假设 N 为3,则物理时间轴 t 长度为 N*Tr,因为 t 原点从0开始,所以 t 的范围为 [0, Tr),既 [1, Tr-ts]。间隔为 ts。
t = 0:ts:N * Tr - ts;
可见,物理时间轴表示方法相较于发射信号没有变化。回波信号的表示方法与发射信号的表示方法的区别主要在于rect窗:
在回波信号中,rect的原理是将 t 时间轴 [t_r, tau + t_r] 部分置为1,其余部分置为0。
t = 0:ts:Tr - ts;
rect = zeros(1, length(t));
for i = 1:length(t)
if t(i) >= (0 + t_r) && t(i) <= (tau + t_r)
rect(i) = 1;
end
end
同样的,使用repmat函数重复rect窗。
Signal_Radar = repmat(rect, 1, N);
干扰信号的时间轴仿真
干扰信号相较于回波信号有一个转发时延 dlt_t ,转发时延可以理解为目标发射干扰信号的时延。
同样的,干扰信号与回波信号时间轴的区别在于rect窗。
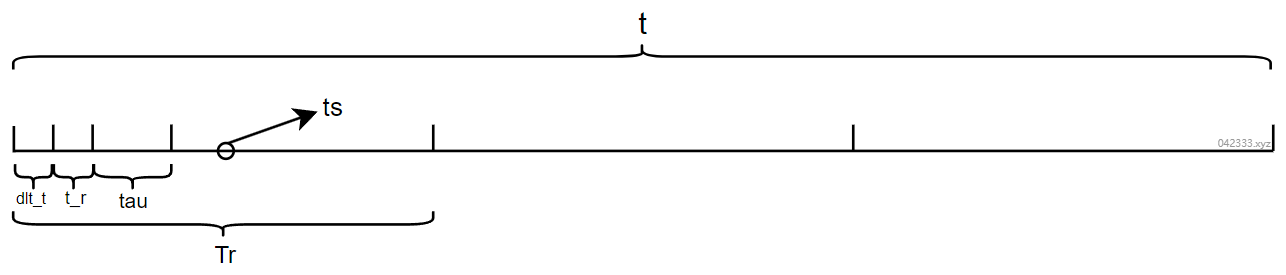
在回波信号中,rect的原理是将 t 时间轴 [t_r + dlt_t, tau + t_r + dlt_t] 部分置为1,其余部分置为0。
t = 0:ts:Tr-ts;
rect = zeros(1, length(t));
for i = 1:length(t)
if t(i) >= (0 + t_r+ dlt_t) && t(i) <= (tau + t_r+ dlt_t)
rect(i) = 1;
end
end
t = 0:ts:N * Tr-ts;
Signal_Radar = repmat(rect, 1, N);
LFM信号的仿真
LFM信号仿真
LFM信号时域的复数表达形式可以表示为:
$$ s(t)=Arect*exp(j2\pi (f_ot+0.5kt^2)+\varphi _0) $$ $$其中,A为幅值,rect为窗函数,f_o为中心频率,k为调频斜率,\varphi _0为初始相位(设为0)$$调频斜率k可以表示为: $$ k=\frac{B}{tau} $$ 其中,B为信号带宽,tau为脉冲宽度
S = exp(1j * 2 * pi * (fo * t + 0.5 * k * (t).^2));
S = Signal_Radar .* S; % Signal_Radar是窗函数
LFM信号时域的普通表达形式可以表示为:
$$ s(t) = Arect*cos(2 \pi f_o (t) + 2 \pi 0.5 k t^2) $$S = cos(2 * pi * fo * t + 2 * pi * 0.5 * k * (t).^2);
S = Signal_Radar .* S;
